кореляційний аналіз

Кореляції про нний ан а ліз, сукупність заснованих на математичній теорії кореляції методів виявлення кореляційної залежності між двома випадковими ознаками або факторами. К. а. експериментальних даних містить в собі такі основні практичні прийоми: 1) побудова кореляційного поля і складання кореляційної таблиці; 2) обчислення вибіркових коефіцієнтів кореляції або кореляційного відношення; 3) перевірка статистичної гіпотези значущості зв'язку. Подальше дослідження полягає у встановленні конкретного виду залежності між величинами (див. регресійний аналіз ). Залежність між трьома і великим числом випадкових ознак або чинників вивчається методами багатовимірного К. а. (Обчислення приватних і множинних коефіцієнтів кореляції і кореляційних відносин).

Кореляційне поле і кореляційна таблиця є допоміжними засобами при аналізі вибіркових даних. При нанесенні на координатну площину вибіркових точок отримують кореляційне поле. За характером розташування точок поля можна скласти попередню думку про форму залежності випадкових величин (наприклад, про те, що одна величина в середньому зростає або убуває при зростанні інший). Для чисельної обробки результати зазвичай групують і представляють у формі кореляційної таблиці. У кожній клітині кореляційної таблиці (див. В ст. кореляція в математичній статистиці) наводяться чисельності гц; тих пар (х, у), компоненти яких потрапляють у відповідні інтервали угруповання по кожній змінній.

Припускаючи довжини інтервалів угруповання (по кожному з змінних) рівними між собою, вибирають центри xi (відповідно yj) цих інтервалів і числа nij в якості основи для розрахунків.

Коефіцієнт кореляції і кореляційне відношення дають більш точну інформацію про характер і силу зв'язку, ніж картина кореляційного поля. Вибірковий коефіцієнта кореляції визначають за формулою:

,

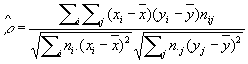де

, ,

, .

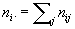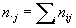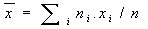При великому числі незалежних спостережень, що підкоряються одному і тому ж розподілу, і при належному виборі інтервалів угрупування коефіцієнт 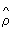близький до істинного коефіцієнту кореляції r. Тому використання як заходи зв'язку має чітко певний сенс для тих розподілів, для яких природною мірою залежності служить r (т. е. для нормальних або близьких до них розподілів). У всіх ін. Випадках в якості характеристики сили зв'язку рекомендується використовувати кореляційне відношення h, інтерпретація якого не залежить від виду досліджуваної залежності.

вибіркове значення 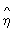y | x обчислюється за даними кореляційної таблиці:

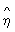2y | x =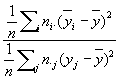

де чисельник характеризує розсіювання умовних середніх значень 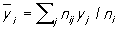близько безумовного середнього (Аналогічно визначається вибіркове значення x | y). величина 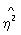y | x використовується в якості запобіжного відхилення залежності від лінійної, т. к. зазвичай 2y | x> r2, 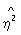x | y> r2 і лише в разі лінійної залежності r 2 = 2y | x = 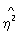x | y. Так, при аналізі кореляції між висотою і діаметром північної сосни було виявлено, що умовні середні значення висоти сосни для заданого діаметра пов'язані нелінійної залежністю. Кореляційне відношення (висоти до діаметру) в цьому випадку дорівнює 0,813, а коефіцієнт кореляції дорівнює 0,762.

Перевірка гіпотези значущості зв'язку грунтується на знанні законів розподілу вибіркових кореляційних характеристик. У разі нормального розподілу величина вибіркового коефіцієнта кореляції 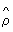вважається значимо відмінною від нуля, якщо виконується нерівність

,

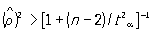де ta є критичне значення t-розподілу Стьюдента з (n- 2) ступенями свободи, відповідне обраному рівнем значущості a (див. Стьюдента розподіл ). Якщо ж відомо, що r ¹ 0, то необхідно скористатися z -Перетворення Фішера (не залежних від r і n):

.

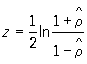Виходячи з наближеною нормальності z, можна визначити довірчі інтервали для істинного коефіцієнта кореляції r.

У разі коли вивчаються не кількісні ознаки, а якісні, звичайні заходи залежності не годяться. Однак, якщо вдається якимось чином впорядкувати об'єкти, що вивчаються щодо деякої ознаки, т. Е. Прописати їм порядкові номери - ранги (по два номери відповідно до двома ознаками), то в якості вибіркової характеристики зв'язку можна скористатися, наприклад, т. н. коефіцієнтом рангової кореляції:

,

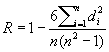де di - різниця рангів за обома ознаками для кожного об'єкта. За ступенем ухилення R від нуля можна зробити деякий висновок про ступінь залежності якісних ознак. Перевірка гіпотези незалежності ознак при невеликому обсязі вибірки проводиться за допомогою спеціальних таблиць, а при n> 10 для обчислення критичних значень вибіркових коефіцієнтів користуються тим, що ці величини розподілені приблизно нормально.

Літ. см. при ст. кореляція .

А. В. Прохоров.