Статистичний контроль якості продукції

У статті розглядаються основні принципи статистичного контролю якості продукції, що існує парадокс його застосування.

1. Основи статистичного контролю якості

Загальновідомо, що один з основних інструментів в боротьбі за ринки збуту - якість продукції. Вже набили оскому « міжнародні стандарти якості ІСО-9000 ». Однак, при цьому, мало хто розуміє, що вони все засновані на сучасних статистичних методах обробки даних. На це прямо вказують як звіти, складені Комітетом ІСО з вивчення принципів стандартизації, так і висловлювання фахівців. Каору Ісікава, заслужений професор Токійського університету, говорить, що для впровадження управління якістю методи статистики - необхідний засіб. І все, починаючи від Ради Директорів і до простого робітника, зобов'язані знати хоча б їх основи.

Отже, що ж таке статистичний контроль якості? Статистичний контроль якості - вибірковий контроль продукції на науковій основі. З огляду на те, що большості методів контролю - руйнують або несопостовіми за вартістю з ціною продукції, в більшості випадків робити суцільний контроль не представляється можливим. І саме на етапі визначення кількості контрольованих виробів, тобто вибірки, і методу їх відбору, вперше з'являються методи математичної статистики і теорії ймовірностей. А, оскільки рішення про придатність або непридатність партії продукції приймається на основі вибірки невеликої кількості одиниць, то така вибірка повинна бути репрезентативною (представницької). Відповідь на питання про відповідність партії може дати тільки теорія ймовірностей.

Найпоширенішими є такі ймовірні моделі: гіпергеометрична і Біноміальна.

У біномінальної моделі вважається, що ймовірність присутності дефектної одиниці однакова при будь-якому методі вибірки однакової кількості одиниць. Тобто візьмемо ми поспіль n штук на початку партії, в кінці партії або вроздріб, ніякого впливу на відсоток бракованих виробів у вибірці не надається. Найвідомішим випадком біноміальної моделі є так зване «нормальний розподіл». Хоч ця модель є більш легкою для розуміння і «ручного» застосування, на практиці вона програє гіпергеометричною моделі.

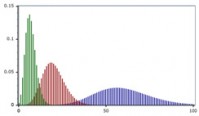
У гіпергеометричною моделі вважається, що ймовірність присутності дефектної одиниці залежить від методу вибірки і випадковість виявляється лише при складанні вибірки. Говорячи простою мовою, якщо ми візьмемо перші n штук виробів з партії, то по біноміальної моделі ця вибірка є репрезентативною, а по гіпергеометричною - не є.

гіпергеометричний розподіл

2. Плани статистичного контролю.

План статистичного контролю - це алгоритм дій по вибірці, аналізу і ухвалення рішення про приймання і бракування партії продукції. При цьому, на вході ми маємо партію (генеральну сукупність), а результатом буде або рішення «прийняти», або рішення «забракувати».

Плани контролю бувають як одноступінчасті, так і багатоступінчасті.

Одноступінчатий план контролю (n, x) означає, що при вибірці n одиниць з партії допускається не більше x дефектних. Число x називають приймальним.

Двоступеневий план контролю (n, x, d) + (m, c) означає, що якщо при вибірці n одиниць є два рівня кількості дефектних: x - при кількості бракованих менш якого партія приймається і d - при кількості яких береться повторна вибірка обсягу m і приймальним числом c.

Основна властивість плану контролю - оперативна характеристика. Вона відображає ризики забраковиванія відповідної партії (або ризик постачальника) і ризики прийняття невідповідної партії (або ризик споживача).

Одним з механізмів спрощення контролю є усічені плани статистичного контролю. Усічений план - такий план контролю, при виконанні якого контроль можна припинити, коли результат стає відомий раніше, ніж відбудеться перевірка всієї контрольної вибірки. Наприклад: якщо є план контролю (60,2) і відразу попалися три бракованих вироби, перевіряти інші не має сенсу, так як вже ясно, що партію слід бракувати.

3. Парадокс класичного статистичного контролю.

Відповідно до класичної теорії, чим вище рівень якості, тим більший обсяг контролю необхідно виконати. І в кінцевому рахунку це може призвести до неможливості класичного статистичного контролю. Розглянемо ситуацію на простому прикладі.

Якщо застосовувати найбільш строгий план контролю виду (n, 0) і використовувати біноміальними модель розподілу, то з достатнім рівнем наближення можна вважати, що необхідний розмір вибірки n становить 2,30 / p, де p - необхідний рівень дефектності. тоді:

· При рівні шлюбу 0,1 (10% або 1 бракована одиниця на 10 придатних) обсяг вибірки складе 23 штуки;

· При рівні шлюбу 0,01 (1% або 1 бракована одиниця на 100 придатних) обсяг вибірки складе 230 штук;

· При рівні шлюбу 0,001 (0,1% або 1 бракована одиниця на 1000 придатних) обсяг вибірки складе 2300 штук;

· При рівні шлюбу 0,0001 (0,01% або 1 бракована на 10000 придатних) обсяг вибірки складе 23000 штук ...

і так далі. В результаті, при наявності одного дефекту на 1 мільйон, вибрати необхідно понад 2 мільйонів одиниць продукції. Таким чином, мова вже може йти тільки про суцільному контролі. Однак, якщо контроль витратний або може бути виконаний тільки руйнівними методами, виходить глухий кут, вихід з якого в рамках класичного статистичного контролю неможливий.

Таким чином, реальний рівень виявлення дефектності класичного статистичного контролю становить не більше 2-2,3%. У сучасних умовах цей рівень вже стає неприйнятним. І тут на допомогу приходять інші, більш сучасні методи статистичного контролю: статистичний контроль технологічних процесів.