Фізична хімія

Процеси, які полягають у перетворенні однієї фази даної речовини в іншу фазу того ж речовини і, отже, що протікають без хімічних реакцій, називаються фазовими перетвореннями (плавлення, сублімація, поліморфні перетворення).

Основною характеристикою фазового перетворення є температура, при якій фази знаходяться в рівновазі. Ця температура залежить від тиску. Так, температура плавлення льоду або, наприклад, температура переходу α-заліза в γ-залізо змінюються в залежності від тиску. При даній температурі тиск насиченої пари (в рівновазі з рідиною) має цілком певне значення. Стан рівноваги визначається зв'язком між рівноважної температурою і рівноважним тиском.

Для знаходження зв'язку з цим врахуємо, що при співіснуванні двох фаз (1 і 2) одного і того ж речовини при постійних р і Т їх молярні енергії Гіббса G 1 і G 2 рівні. Тому умовою рівноваги між двома фазами при малих змінах р і Т є рівність d G 1 = d G 2. Відповідно до рівняння (II.32)

V 1d p + S 1d T = V 2d p - S 2d T,

де V 1 і V 2 - молярні об'єми;

S 1 і S 2 - молярні ентропії. Звідси слідує що

= =,

де Δ V і Δ S - зміни обсягу і ентропії при ізотермічному фазовому перетворенні одного благаючи речовини.

Хоча при фазовому перетворенні обсяг змінюється, тиск залишається постійним. Наприклад, при випаровуванні рідини, що відбувається при постійній температурі, тиск пара не змінюється. Тому похідна в лівій частині останнього рівняння є повною.

Так як процес фазового перетворення є ізотермічним і рівноважним, то Δ S = Q / T і

d p / d T = Q / T Δ V, (III.1)

де Q - тепло, що надається системі при перетворенні.

Для рівноваги рідина - пар рівняння (III.1) дає залежність пружності насиченої пари від температури, а також температури кипіння від тиску. Оскільки V 2п більше V 1Ж і при перетворенні рідини в пар надається тепло Q, то похідна d p / d T позитивна і, отже, з підвищенням температури тиск пара має збільшуватися. Величина Q тут дорівнює Δ H ісп, часто позначається λ.

Такі ж наслідки з рівняння (III.1) можна отримати для рівноваги тверде тіло-пар, де Q відповідає ентальпії сублімації Δ H суб (σ).

Для рівноваги в системі тверда фаза (1) - рідина (2) рівняння (III.1) дає залежність температури плавлення від тиску:

d T / d p = T (V 2 - V 1) / Q.

При переході 1 → 2 тепло надається системі, і Q (ентальпія плавлення Δ H пл) позитивна (Δ H пл позначають і буквою ρ). Отже, знак похідної залежить від різниці обсягів твердої і рідкої фаз. Якщо при плавленні обсяг збільшується (V 2> V 1), то з ростом тиску температура плавлення буде підвищуватися. Якщо ж V 2 <V 1, то з підвищенням тиску температура плавлення повинна зменшуватися.

У більшості речовин різницю (V 2 - V 1) позитивна. Виняток становлять Н2О, Bi, Ga і деякі марки чавуну. При перетворенні лід - рідка вода обсяг зменшується (Δ V - негативна величина), тому температура плавлення льоду знижується при збільшенні тиску (на 0,007 ° C при зростанні тиску на 1 ат).

Застосування рівняння (III.1) для аллотропических перетворень можна ілюструвати на прикладі перетворення заліза з α- в γ-модифікацію, яке при атмосферному

тиску відбувається при 910 ° C. Це перетворення супроводжується поглинанням тепла (900 Дж / моль). Щільність α-Fe складає 7,571 г / см3, а γ-Fe 7,633 г / см3. Щоб отримати розмірність величини d T / d p в градусах на атмосферу або на 105 Па, слід теплоту процесу висловити в л · Па · 105, а зміна обсягу при перетворенні в л. З огляду на, що 1 Дж еквівалентний 9,8 · 10-3 л · Па · 105, для одного благаючи атомів. Fe

Δ V = 55,85 (

-) = -0,06 см3 = -0,06 / 1000 л. = - (910 + 273) · 0,06 900 · 9,8 · 10-3 · 1000 = -0,0080 K / 105 Па,

тобто при збільшенні тиску на одну атмосферу (105 Па) температура перетворення α-γ зменшується на 0,0080 К. Слід, однак, мати на увазі, що наведений розрахунок носить спрощений характер, так як в ньому не береться до уваги залежність теплоти перетворення від температури , а температура береться постійною. Тому він дає точні результати лише при порівняно невеликих змінах тиску.

Рівняння (III.1) було знайдено Клапейроном ще до відкриття першого закону термодинаміки і потім виведено Клаузиусом і носить назву рівняння Клапейрона-Клаузіуса. Це рівняння дозволяє знайти важливу для практики залежність тиску насиченої пари рідини або твердого тіла від температури. Для першого випадку

Якщо Т значно нижче критичної, то величиною об'єму рідини можна знехтувати в порівнянні з величиною обсягу пара. Крім того, за умови, що пар поводиться як ідеальний газ V п = RT / p, звідки (1 / р) (d p / a T) = = Δ H ісп / RT 2 або

d ln p / d T = Δ H ісп / RT 2, (III.2) 1

і наостанок,

ln p = ∫ d T + C, (III.3)

де С - постійна.

Очевидно, для тиску насиченої пари твердого тіла рівняння (III.2) має вигляд: d ln p / d T = Δ H cyб / RT 2, де Δ H суб - ентальпія сублімації (σ).

Замінюючи натуральний логарифм в рівнянні (III.3) десятковим, отримаємо:

lg p = 1 / 19,14 ∫ + i. (III.4) *

Постійна інтегрування I називається хімічної постійною. Для знаходження пружності пара необхідне знання величини i і залежності Δ H ісп від температури. Як і для будь-якого теплового ефекту, температурна залежність теплоти випаровування описується рівнянням. Кирхгофа:

dΔ H ісп / d T = С рп - З рж, (III.5)

яке, як зазначалося, не зовсім точно.

В якості першого наближення приймемо, що теплоємності пара і рідини рівні. В цьому випадку Δ H ісп не залежить від температури, і з рівняння (III.4) слід, що

lg p = -Δ H ісп / 19,14 T + i. (III.6)

Природно, що внаслідок прийнятого допущення це рівняння грубо наближено і може дати задовільну точність лише при використанні в невеликому інтервалі температур, в якому величина Δ H ісп практично постійна. У цьому випадку для отримання залежності р від Т необхідно знати дві величини: Δ H ісп і i

Рівняння (III.6) часто використовують в якості интерполяционного в такій формі: lg p = (A / T) + B, де А і В - постійні. У деяких випадках подібні рівняння дають задовільну точність у відносно великому інтервалі температур. Так, наприклад, тиск пара рідкого алюмінію при 1290 К становить 10-11 Па, а при 1 545 · 10-7 Па.

Потрібно знайти тиск пара, наприклад, при 1405 К. Знайдемо спочатку значення А і В з двох рівнянь для 1290 і 1545 К:

- 11 = (A / 1290) + В і -7 = (A / 1 545) + В;
A = -15636 і В = 6,118.

Звідси шукана величина lg p =

+ 6,118 = -5,008, тобто р ≈ 10-5 Па.

Інший спосіб наближеного обчислення тиску пара вимагає знання ентальпії випаровування і температури кипіння даної речовини. Так, для алюмінію ентальпія випаровування становить 299 156 Дж / моль, а температура кипіння 2600 К. При температурі кипіння тиск насиченої пари над рідиною досягає зовнішнього атмосферного і дорівнює одиниці. Підставляючи ці значення в рівняння (III.6), знайдемо:

0 = -

+ I, тобто i = 6,01.

Звідси для температури 1405 К

lg p = -

+ 6,01 = -5,11.

Невелика відмінність від отриманого вище результату пояснюється тим, що в другому випадку інтерполяція проводилася в більш широкому інтервалі температур.

У тих випадках, коли відсутні дані про теплотах випаровування рідин, для наближеної оцінки цієї величини може бути використано емпіричне правило трутони. Згідно з цим правилом, для багатьох рідин відношення теплоти випаровування до абсолютної температурі кипіння є величина постійна, близька до 22, т. Е. Δ H ісп / T кип = 22 1 .

Правило трутони задовільно виконується для неасоційованих рідин. Теоретично більш обгрунтовано правило Гільдебрандт, згідно з яким для рідин відносини теплоти випаровування до абсолютної температурі однакові при температурах, при яких однакові концентрації парів.

Для оцінки тиску пара може бути використано емпіричне правило Дюринга, що встановлює, що ставлення абсолютних температур, при яких тиск парів двох подібних речовин однаково, є величина постійна. Так, наприклад, температури кипіння заліза і марганцю відповідно рівні 3008 і 2370 К і їхнє ставлення 3008/2370 = 1,27. Знаючи, що при 2277 К тиск пара заліза одно 103 Па, можна знайти температуру (2277 / 1,27 = 1792 К), при якій тиск пари марганцю матиме таке ж значення, що порівняно близько до спостерігається величиною (1750 К).

Для більш суворого рішення задачі про залежність тиску

пара від температури слід враховувати, що теплоємності конденсованої фази (рідкої або твердої) і пара неоднакові і залежать від температури, тобто dΔ H ісп / d T = Ср (п) - Ср (конд), або в інтегрованій формі:

Δ H ісп = Δ H 0 +

[Ср

(п) - Ср (конд)] d T,

де Δ H 0 - постійна.

Підставляючи цей вираз в рівняння (III.4), отримаємо:

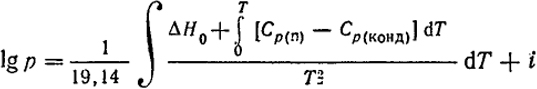
4), отримаємо:

(III.7) 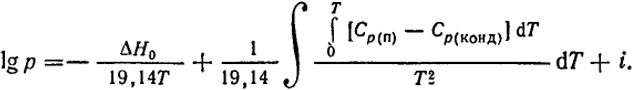(III (III.8)

Таким чином, щоб знайти рівняння, що зв'язує тиск пара і температуру в будь-якому інтервалі температур, необхідно знати теплоємності пара і конденсованої фази в залежності від температури в цьому інтервалі, теплоту випаровування і тиск пари при одній температурі. В якості другого наближення при вирішенні цього завдання приймається, що теплоємності не залежить від температури, тоді з рівняння (III.8) слід:

lg p = + Cр (п) - Ср (конд) 19,14 lg T + i (III.9)

Для вирішення ряду завдань важливо визначити ентальпію (теплоту) випаровування і сублімації. Для речовин, у яких ці перетворення відбуваються при високих температурах, наприклад, для металів, особливо тугоплавких, калориметричні вимірювання Δ H ісп і Δ H суб вельми важкі. У цих випадках зазначені величини знаходять з вимірювань тиску пара при різних температурах.

Рівняння (III.2) може бути переписано у вигляді:

= -Δ H ісп / R,

звідки випливає, що графічно величини Δ H ісп або Δ H суб

можуть бути знайдені з значення тангенса кута нахилу дотичної до лінії, побудованої в координатах ln p - (l / T). Якщо ця лінія крива, то отримане значення Δ H ісп відноситься до температури, відповідної точці дотику. На рис. III.1 представлена залежність логарифма парціального тиску рідкого заліза від l / T.

Множник 19,14 є твір універсальної газової постійної R = 8,314 Дж / моль і коефіцієнта переходу від натуральних логарифмів до десятковим, рівного 2,303. 1 Тут Δ H ісп слід висловлювати в кал.