Вплив математичної діяльності на формування пізнавальних процесів старших дошкільників

сучасна освіта

Ремнева Н.А., Стожарова М.Ю. - Вплив математичної діяльності на формування пізнавальних процесів старших дошкільників // Сучасна освіта. - 2012. - № 1. - С. 68 - 78. DOI: 10.7256 / 2306-4188.2012.1.211 URL: https://nbpublish.com/library_read_article.php?id=211

Вплив математичної діяльності на формування пізнавальних процесів старших дошкільників

Анотація.

Дата направлення до редакції:

Дата рецензування:

Дата публікації:

Abstract.

Keywords:

Актуальність проблеми формування пізнавальних процесів у дошкільній освіті

Проблема формування пізнавальних процесів - одна з пріоритетних завдань дошкільної освіти. Актуальність даної теми обумовлена, по-перше, соціальним замовленням у сфері освіти, який відображає зростаючу потребу держави і суспільства в підготовці кваліфікованих фахівців, які вміють продуктивно мислити. У зв'язку з цим в даний час особливого значення набувають вимоги до якісно нового рівня розвитку пізнавальних процесів, в тому числі і на етапі дошкільної освіти. По-друге, від якості знань і умінь, від рівня пізнавальних процесів і пізнавальної активності дитини, сформованих в дошкільні роки, залежить розвиток шкільної зрілості старшого дошкільника, а, отже, і успішність подальшого навчання в школі. Адже дошкільний вік є сенситивним періодом для розвитку пам'яті, уваги, мислення, мовлення, саме в цьому віці закладається фундамент формування особистості.

Аналізуючи існуючі підходи до визначення поняття (И.В.Дубровина, Л. І. Божович, Е.Е.Кравцова, Н.В.Ніжегородцева, В.Д.Шадріков, Н.И.Гуткиной, Л.А.Венгер, Л .С.Виготскій і ін.), шкільна зрілість являє собою багатофункціональний складне структурне утворення, яке включає, перш за все, зрілість в інтелектуальному, емоційному та соціальному відносинах. [5]

Саме під інтелектуальної готовністю як одним з компонентів шкільної зрілості слід розуміти необхідний рівень розвитку деяких пізнавальних процесів: мислення, пам'яті, уваги, мови і т.д.

Математична діяльність - потужний засіб інтелектуального розвитку дошкільника

Виникають два питання: чи впливає математична діяльність на формування пізнавальних процесів? Як сформувати пізнавальні процеси старших дошкільників в математичної діяльності в умовах дошкільного закладу? Зупинимося на першому питанні.

Аналіз наукових досліджень педагогічного досвіду (А.М.Леушіна, Н.І.Непомнящая, А.А.Столяр і ін.) Переконує в тому, що раціонально організоване навчання дошкільнят математиці забезпечує загальний розумовий розвиток дітей. [7]

Дослідники А.В. Брушлинский, А.Н. Колмогоров, В.А. Крутецкий, В.В. Давидов, З.І. Калмикова, А.Я. Хинчин, Ю.М. Колягин, Л.В. Виноградова, І.В. Дубровіна та ін. Відзначають такі специфічні особливості розумового процесу у старших дошкільників в процесі формування первинних математичних уявлень як гнучкість розумових процесів, тобто нешаблонность, неординарність, уміння варіювати способи вирішення пізнавальної проблеми, легкість переходу від одного шляхи вирішення до іншого, вміння виходити за межі звичного способу діяльності і вміння знаходити нові способи вирішення проблеми при змінених умовах. [3]

У радянській психології термін «гнучкість мислення» ввела в практику Н.А.Менчинская і Д.Н.Богоявленский виділили три основні показники гнучкості мислення:

• Доцільне варіювання способів дії;
• Легкість перебудови знань і навичок і їх систем відповідно до змінених умов;
• Легке перемикання від одного способу дії до іншого. [1]

Дослідники виділяють також таку характеристику, як глибина мислення, тобто уміння проникати в суть кожного досліджуваного факту і явища, вміння бачити їх взаємозв'язок з іншими явищами.

В.А. Крутецкий говорив про розвиток математичних здібностей як про індивідуально-психологічних особливостях людини, що допомагають йому при інших рівних умовах щодо швидше, краще і глибше оволодівати знаннями, вміннями і навичками в області математики. [7]

Російські психологи С.Л.Рубинштейн і А.М.Матюшкин стверджували, що у дітей розвивається математичне мислення, яке має такі особливості:

1. Схильність до операцій з числами і на ще більш високому рівні схильність і інтерес до математичних проблем;
2. Швидкість засвоєння рахункових правил;
3. Особливо сильне розвиток абстрактного мислення, аналітико-синтетичних комбінаційних здібностей в області оперування числовою і знаковою символікою;
4. Розвивається самостійність і оригінальність у вирішенні математичних проблем і посилення творчого мислення;
5. Вольову активність і працездатність в області математичного праці;
6. Перехід схильності і інтересу в захоплення, коли математична робота стає покликанням;
7. Продуктивну за кількістю і якістю діяльність, що дозволяє виявити всі більш випереджають однолітків показники. [2]

Михайлова З.А. підкреслювала особливе значення цікавих завдань (завдань-смекалок) в розвитку елементів математичного мислення дошкільників (математичної ініціативи, кмітливості, логічності, гнучкості, критичності розуму). До вирішення цікавих завдань діти приходять в процесі пошукових проб. Причому дії дітей мають різний характер: це практичні проби, призначені для вгадування рішення в результаті постійних дій. Більшість дітей в залежності від віку та рівня мислення вирішують завдання в розумі, цьому сприяє різнобічний аналіз. Під впливом навчання характер пошукових дій зазнає суттєвих змін: діти переходять від практичних до уявним пробам, зменшується їх кількість, так як виробляються вміння. Результатом пошуку рішення є здогад, яка представляє собою перебування шляхи подолання.

Прояв дітьми кмітливості та кмітливості при вирішенні завдань зростає в міру оволодіння дітьми певними схемами аналізу, перенесення засвоєних загальних принципів, способів вирішення простих завдань на більш складні.

Навчання рішенню цікавих завдань сприяє розвитку самостійності дітей. Дитина, що вирішує завдання, на основі наявних у нього знань, умінь, засвоєних принципів рішення, логіки проявляє кмітливість, самостійність, що допомагає йому знайти правильну відповідь. [4]

Уже в ранньому дитинстві починають складатися уявлення про навколишній, про ознаки і властивості предметного світу: форму, величину, просторове розташування предметів і їх кількості. В основі пізнання маленькими дітьми якісних та кількісних ознак предметів і явищ лежать сенсорні процеси: відчуття, сприйняття, уявлення. Сенсорний розвиток - перша сходинка інтелектуального розвитку. Без вирішення цього завдання неможливо подальше розумовий розвиток. У дошкільному віці здійснюється освоєння сенсорних еталонів не тільки на перцептивном, а й на інтелектуальному рівні (Л. А. Венгер). Маленькі діти опановують окремими елементами системи еталонів, застосовуючи обслідницькі дії, яким їх навчали дорослі. Більш старші дошкільнята, використовуючи сериацию і класифікацію, приходять до усвідомлення принципу побудови таких систем.

[6]

Процес формування елементарних математичних уявлень передбачає планомірне засвоєння і поступове розширення словникового запасу, вдосконалення граматичного ладу і зв'язності мовлення.
Наприклад, кількісні відносини дитина відображає за допомогою слів багато, один, жодного, стільки, скільки, порівну, більше, менше і т. Д., Які усвідомлюються в результаті безпосередніх дій при порівнянні окремих предметів і їх сукупностей. Запозичені з промови оточуючих слова-числівники наповнюються сенсом і використовуються з певною метою - дізнатися, скільки предметів. За рахунку дитина вчиться на інтуїтивному рівні погоджувати числівник з іменником в роді, числі і відмінку. Відбувається збагачення мови і за рахунок оволодіння деякими спеціальними термінами (назви арифметичних дій, загальноприйнятих одиниць виміру, геометричних фігур і т. Д.). Їх обсяг вкрай незначний, так як основний зміст промови дітей становить «чисто» побутової словник.
При формуванні математичних уявлень мовленнєвий розвиток відбувається не ізольовано, а у взаємозв'язку з сенсорними і розумовими процесами. [8]

Таким чином, можна зробити висновок, що процес формування елементарних математичних уявлень сприяє розвитку пізнавальних процесів дошкільнят:

* Планомірне засвоєння і поступове розширення словникового запасу, розвиток зв'язного мовлення;

* Розвиток мислення, розумових операцій (узагальнення, класифікація, синтез, аналіз І.Д.);

* Сенсорний розвиток дошкільнят.

Організація експериментальної роботи

Тепер відповімо на друге питання: як же сформувати пізнавальні процеси старших дошкільників в математичній діяльності?

У нашому дослідженні формування первинних математичних уявлень є потужним засобом розвитку пізнавальних процесів дошкільника, його творчих здібностей. Ми розглядаємо математику не тільки як правильно організовану діяльність, що забезпечує своєчасне математичне розвиток дошкільника, а як інтелектуально-розвиваючу технологію, як засіб розвитку всіх психічних процесів.

Ми вважаємо, що формування пізнавальних процесів старших дошкільників буде ефективно за умови спеціально розробленої системи навчання в дошкільному закладі, а саме:

1. Поєднання різних видів (лічильна, обчислювальна та вимірювальна діяльність) і форм організації математичної діяльності (безпосередньо освітня діяльність; спільна робота педагога з дітьми; самостійна математична діяльність дітей).

2. Використання методів і засобів навчання, спрямованих на підвищення мотивації старших дошкільників до математики (з включенням варіативних, проблемних, творчих завдань).

3. Створення в ДНЗ спеціальної предметно-розвиваючого середовища (Створення «Куточка цікавої математики», в який помістили різноманітний цікавий матеріал, з тим, щоб кожна дитина змогла вибрати для себе гру).

4. Розробка змісту спільної діяльності вихователів з батьками та педагогів з дітьми.

Нами була проведена експериментальна робота з дітьми старшого дошкільного віку з формування пізнавальних процесів в різних формах організації математичної діяльності. (Розроблено авторську програму по формуванню пізнавальних процесів, а саме уваги і мислення старших дошкільників в різних формах організації математичної діяльності).

Головною метою програми є розвиток уваги і мислення старших дошкільників за допомогою різноманітних ігор та вправ математичного змісту.

Основними завданнями програми є:

- формування логічного мислення старших дошкільників;

- формування прийомів розумових дій (аналіз, синтез, порівняння, узагальнення, класифікація, аналогія);

- збільшення обсягу уваги;

- розвиток вміння зберігати стан уваги на якомусь об'єкті, предметі; переводити свою увагу з одного об'єкта на інший; паралельно виконувати декілька видів діяльності;

- вироблення вміння цілеспрямовано володіти вольовими зусиллями, встановлювати правильні стосунки з однолітками і дорослими, бачити себе очима оточуючих.

Ці завдання вирішуються в процесі ознайомлення дітей з різними областями математичної дійсності: з кількістю, і за числом, вимірюванням і порівнянням величин, просторовими і тимчасовими орієнтування. Нове знання не дається дітям в готовому вигляді, а осягається ними шляхом самостійного аналізу, порівняння, виявлення істотних ознак. Таким чином, математика входить в життя дітей як «відкриття» закономірних зв'язків і відносин навколишнього світу. А вихователь підводить дітей до цих «відкриттів», організовуючи і направляючи їх пошукові дії.

висновки

Зіставлення результатів вимірів, проведених в експериментальній і контрольній групах до і після закінчення експериментальної роботи (див. Рис.1) наочно демонструє результативність пропонованої Програми розвитку пізнавальних процесів дітей старшого дошкільного віку.

Рівень розвитку пізнавальних процесів (мислення і уваги) старших дошкільнят

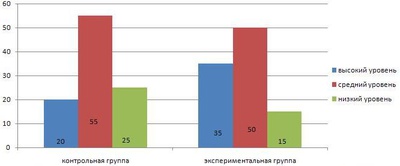
Рис.1. Розподіл дошкільнят-респондентів за рівнями розвитку пізнавальних процесів (мислення і уваги) в експериментальній і контрольній групах

Таким чином, проведений експеримент підтвердив наше припущення про вплив математичної діяльності на формування пізнавальних процесів старших дошкільників як одного з компонентів шкільної зрілості: показано, що поєднання різних видів і форм організації математичної діяльності дітей; використання різноманітних методів і засобів навчання, спрямованих на підвищення мотивації старших дошкільників до математики; створення в ДОУ предметно-розвиваючого середовища; розробка змісту спільної діяльності вихователів з батьками та педагогів з дітьми привели до підвищення рівня розвитку пізнавальних процесів, зокрема, уваги і мислення дітей старшого дошкільного віку.

Бібліографія